連立方程式 例題 489680

 定価・原価・利益の問題（連立方程式） 問題文の中に、求める数が2つある場合は、それぞれを 、 で表します。 ただし、問題によっては、求める数に関連のある数を 、 としたほうが解きやすい場合もあります。 問題文から等しい関係にあるものを基礎方程式の離散化 => 連立1次方程式(flow) Q数値解析とは？ A 基礎方程式を離散化して最終的に得られる連立1次方程式を解く． 基礎方程式（1次元Laplace方程式） 差分方程式の代数表示 差分方程式 差分法で離散化 計算領域モデル 境界条件 連立1次方程式2年生 2 連立方程式 知識・技能の習得を図る問題 年 組 号氏名 練習問題① 1 解が（x ，y ）＝（－1，4）になる連立二元一次方程式を1つつくりなさい。 2 解が（x ，y ）＝（2，1）になる連立方程式を次のアからオの中からすべて選びなさい。 ア 2x ＋y ＝1 イ 3x ＋4y ＝10 ウ 2x －3y ＝7

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点

連立方程式 例題

連立方程式 例題-2元1次方程式や連立方程式の意味を理解し、代入法や加減法で、連立方程式を解く練習をする問題プリントです。 連立方程式の解き方 練習問題 （1） 答え 連立方程式の解き方 練習問題 （2） 答え 連立方程式の解き方 練習問題 （3） 答え 連立方程式の連立方程式(計算練習2) 連立方程式を解け y=2x3 3xy=4 5xy=13 4xy=11 5x3y=19 4xy=11 x3y=8 x2y=7 5xy=9 y=2x5 4x7y=1 3x2y=8 2x3y=10 x=y5 12x04y=2 21x04y=46 3(4x2y)=x9 2x3y=6 4 3 x 5 4 y= 1 2 3 2 x 3 4 y= 9 2 1 4 x 1 2 y=1 2 3 x 8 9 y= 4 9 4x3y=2xy6=2

反矩陣公式方塊矩陣 Prdceg

6 文字の入った連立1 次方程式 例題5 以下の連立方程式が解を持つように，aを定めて解を求めよ． x y z= 6 x y 2z= 11 2x 2y− 4z= a （解答） 1 1 1 6 1 1 2 11 2 2 −4 a → 1 1 1 6 0 0 1 5 0 0 −6 a−12 → 1 1 0 1 0 0 1 5 0 0 0 a18「連立方程式の解」とは，左の例 (A) などにおいて2つの方程式を両方とも満たす x , y の値のことです． 連立方程式の解を求めるには，まず，未知数が1つだけ（たとえば x だけ）の方程式を作って，解くことを考えます． x だけの方程式なら解けるからです．例題12 家から学校まで 10 mあります．途中の橋まで毎分 50 mの速さで歩き，橋から学校まで毎分 80 mの速さで歩いたら，合計で 15 分かかりました．家から橋まで，橋から学校までそれぞれ何分歩きましたか． (1) 家から橋まで x 分，橋から学校まで y 分歩い

次の連立方程式を解け。 4x7y2 3 = 9 4 x2y3= 17x11y34 6 aを整数とする。連立方程式 axy=3 3xy=10 の解がともに自然数のとき、定数aの値を求めよ。 連立方程式をたてて求めよ。 原価100円の商品Aと、原価0円の商品Bを合わせて140個仕入れた。連立方程式の文章題（文字の置き方） ＜例題 ＞ 携帯電話を購入し、60分間通話したら、購入代金と通話代金で、合わせて、6000円だった。 また、同じ携帯電話を購入し、1分間通話したら、購入代金と通話代金で、合わせて、9000円だった。 携帯電話のX2 = dx dt

の合同方程式が与えられたとき，上記の例題9, 10のように の剰余類で分類すれば解けるが， が大きな値の場合には，分類が煩雑になるため，この方法だけで解くことは容易でない． 「連立方程式の利用」の文章題を一目で理解できるように、重要事項を最も簡単にまとめました。 1、問題を解くときの順序 (1)何をxとyにするかを決める（ふつう、問題文の最後で「求めなさい」と書かれているものをx、yにする） (2)問題文中で、「文章を等式に表せる部分」を2か所見連立方程式を解け x=2y5 x3y=7 x3y=7 x5y=11 2x3y=8 x5y=11 x2y=4 x3y=7 x2y=10 x=3y5 2x5y=11 3x4y=6 xy=10 x=y4 01x05y=13 03x04y=06 3xy=5 2 (x3y)=14 2 3 x 1 5 y= 8 15 2 5 x 3 10 y= 2 5 1 2 x 2 3 y= 1 6 3 2 x 7 6 y= 13 6 x3y=4x6y=2 解説リクエスト 解説リクエストフォーム 問題名

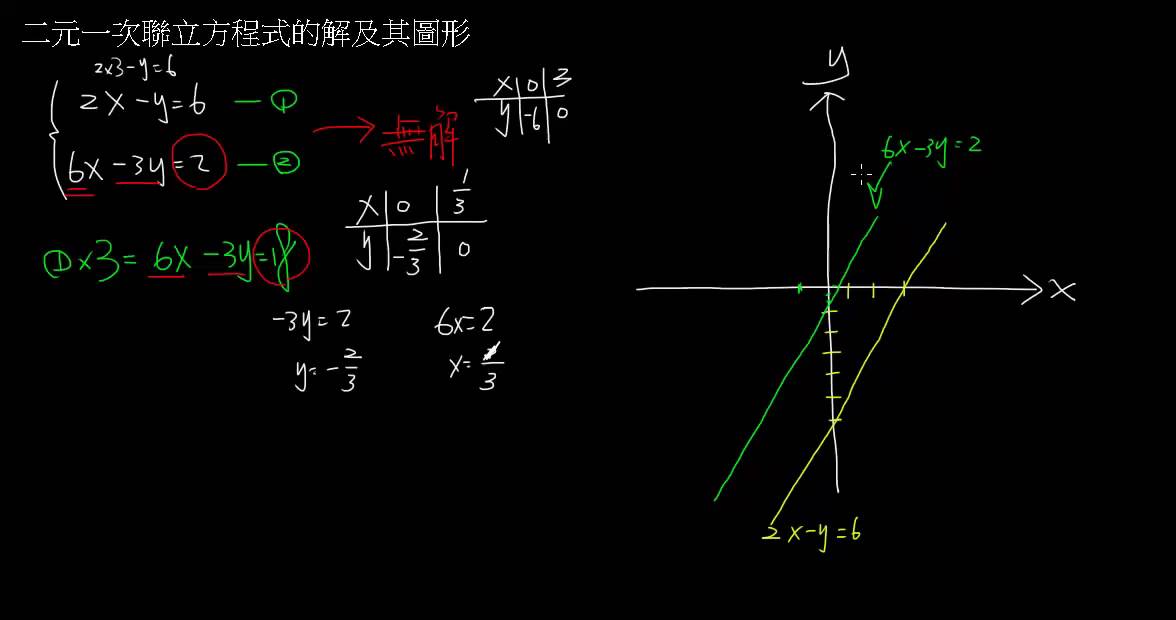
二元一次聯立方程式的解及其圖形 Youtube

中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット

連立一次方程式 例題 以下に示す二元連立一次方程式を①ヤコビ法および②ガウス・ザイデル法で解け。 但し、初期値はx 1 = x 2 = 0、精度ε= 0005 とせよ。 2 2 5 2 4 1 2 1 = = x x x x 二つの方法での近似解の漸化式は以下の様になる。 ① ヤコビ法 () 1 ( ) 1連立方程式の計算は、行列の考え方を利用することで解くことができる。 上記のような連立方程式は以下のように 行列で記述することができる。 とおくと、求めたい 1, 2, 3は 以下のように求めることができる。 連立方程式の計算 28 次のように、3つの式が出てくる連立方程式の解き方について解説していきます。 次の方程式を解きなさい。 $$6x5y=2x3y=4$$ 次の連立方程式を解きなさい。

有名な 2元連立方程式公文

連立一次方程式を掃き出し法で解く6つの例題 理数アラカルト

 連立方程式の式で、 文字が片方によっている連立方程式 は代入法で解いたほうが便利なんだ。 しかも、よっている文字の係数が1ならなお最高！ たとえば次のような連立方程式の問題のときだね。 例題1 つぎの連立方程式を解きなさい。 2x3y=11 y = 5x ガウスの消去法の概要 ガウスの消去法は 前進消去 （文字を1つずつ消していく操作）と 後退代入 （1成分ずつ答えを求めていく操作）からなります。 順々に説明していきます。 注：以下では方程式の数と変数の数が同じで，解が一つしかない（係数行列が正則）場合を考えます。連立方程式 例題 連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく

第1章 連立方程式

第1章 連立方程式

 うさぎでもわかる微分方程式 Part10 連立微分方程式（2階微分方程式に帰着させて解くパターン） 年4月22日 21年7月27日 36分秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回から何回かにわけて連立微分方程式について書いていき うさぎでもわかる微分方程式 Part15 ラプラス変換を用いた微分方程式・連立微分方程式の解き方 年5月2日 21年6月11日 53分35秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は、非同次の定数係数線形微分方程式の4つの解き方 未定係定数係数連立線形常微分方程式— 11 同次方程式 次の形の連立常微分方程式を定数係数連立線形常微分方程式とよぶ： は定数 この方程式を満たすベクトル をこの方程式の解と呼ぶ。 特に 常に の場合、即ち を同次斉次方程式とよぶ。 iv

たかが連立方程式ではあるけれど 大験セミナー わくわく日記

連立方程式の解き方と交点の座標の求め方 数学の偏差値を上げて合格を目指す

3つの文字、式の連立方程式を計算する方法 xy=3,xy=2の和と積の連立方程式の解き方は？ 途中で速さが変わる文章問題の解き方、コツを解説！ 割合を使った全校生徒の増減に関する文章題の解き方を解説！ 池の周りを追いつく速さの問題を解説！←今回の記事2次2次連立形 == 連立方程式の作り方･･･文章題 == 例題1 りんご1個の価格がみかん2個の価格よりも50円高く，みかん3個の価格よりも30円安いものとする． みかん1個の価格を x （円），りんご1個の価格を y （円）とすると， x , y が満たす連立方程式は y分方程式は階数が上がると解くのが難しくなるので階数を下げて連立微分方程式の形に持ち込むということがよ くやられます。余談になりますが，一般に2 階線形微分方程式 d2x dt2 P1(t) dx dt P2(t)x = Q(x) を連立微分方程式にして階数を下げるには， x = x1;

中2数学 ａ ｂ ｃの連立方程式 例題編 映像授業のtry It トライイット

中学数学 連立方程式 加減法 中学数学の無料オンライン学習サイトchu Su

 連立方程式の式のつくり方、具体的に解説 （1）数と量の例題 手順1．問題文を分ける。 手順2．条件をすべて書きだす。 手順3．解りにくいならイラストや表を描いてみる。 手順4．求めるものをx（エックス）とy（ワイ）におきかえる。 手順5連立方程式とは {7x2y =5 2x5y = 8 のように2つ以上の方程式を組み合わせたものが 連立方程式 である。 組み合わせた, どの方程式も成り立たせるような文字の値の組が連立方程式の解となる。 中学で扱うのは上記のような2元1次方程式の連立方程式である。連立方程式 例題 連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく

例題付き 連立方程式の解き方と失敗しないコツ

三元一次聯立方程式 利用克拉瑪公式判斷三平面關係之一 Youtube

 方程式の解き方が分かっていれば、すんなり内容が入ってくると思います。 それでは、例題を使って理解していきましょう！ ＊第1回：院試対策線形代数①（同次連立1次方程式） 行列を用いた解法 最後は連立漸化式の解法における3番に対応する方法です。 n n 変数の1階線形連立微分方程式を考えましょう。 この式を次のように書き換えます。 と書けます。 要素数 \mathbb {x} = e^ {tA} \mathbb {c} x = etAc とすれば，これは解になります

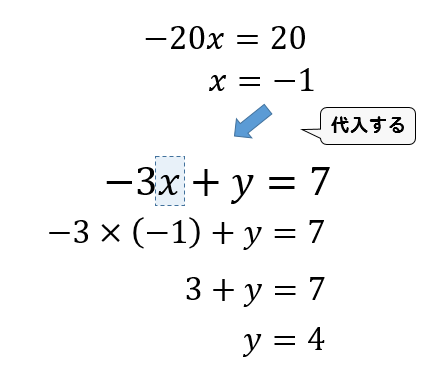
連立方程式３つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト

App Store 上的 中2連立方程式計算問題

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点

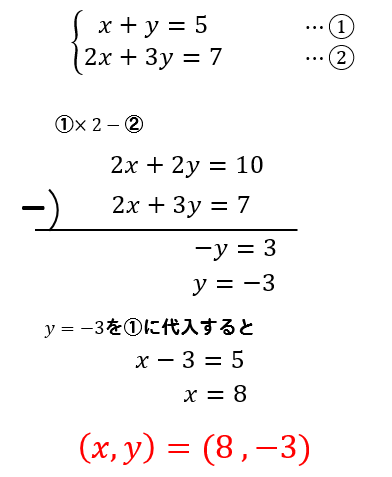
方程式練習問題 連立方程式 A B C 方程式の解き方まとめサイト

トップ100連立方程式公式 最高のカラーリングのアイデア

中２連立方程式の解き方と計算問題 代入法と加減法 Irohabook

第1章 連立方程式

例題 加減消去法2 數學 均一教育平台

例題 克拉瑪公式解二元一次方程組進階 Youtube

一元二次方程式

秋篠理数 算数教室の さあさあ お勉強だよ

有名な 2元連立方程式公文

連立方程式 加減法 代入法の簡単な練習問題 これでテストはバッチリ 数スタ

連立3元1次方程式 まなびの学園

第1章 連立方程式

Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download

2元一次方程式題目初中數學 二元一次方程式 例題2 Gquhm

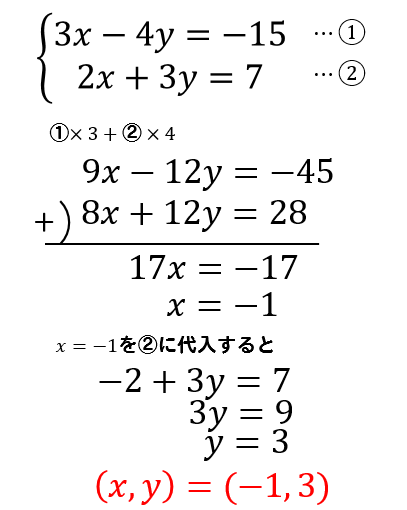
トップ100連立方程式公式 最高のカラーリングのアイデア

反矩陣公式方塊矩陣 Prdceg

中学２年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

App Store 上的 中2連立方程式計算問題

世界一わかりやすい数学問題集中２ ２章 連立方程式

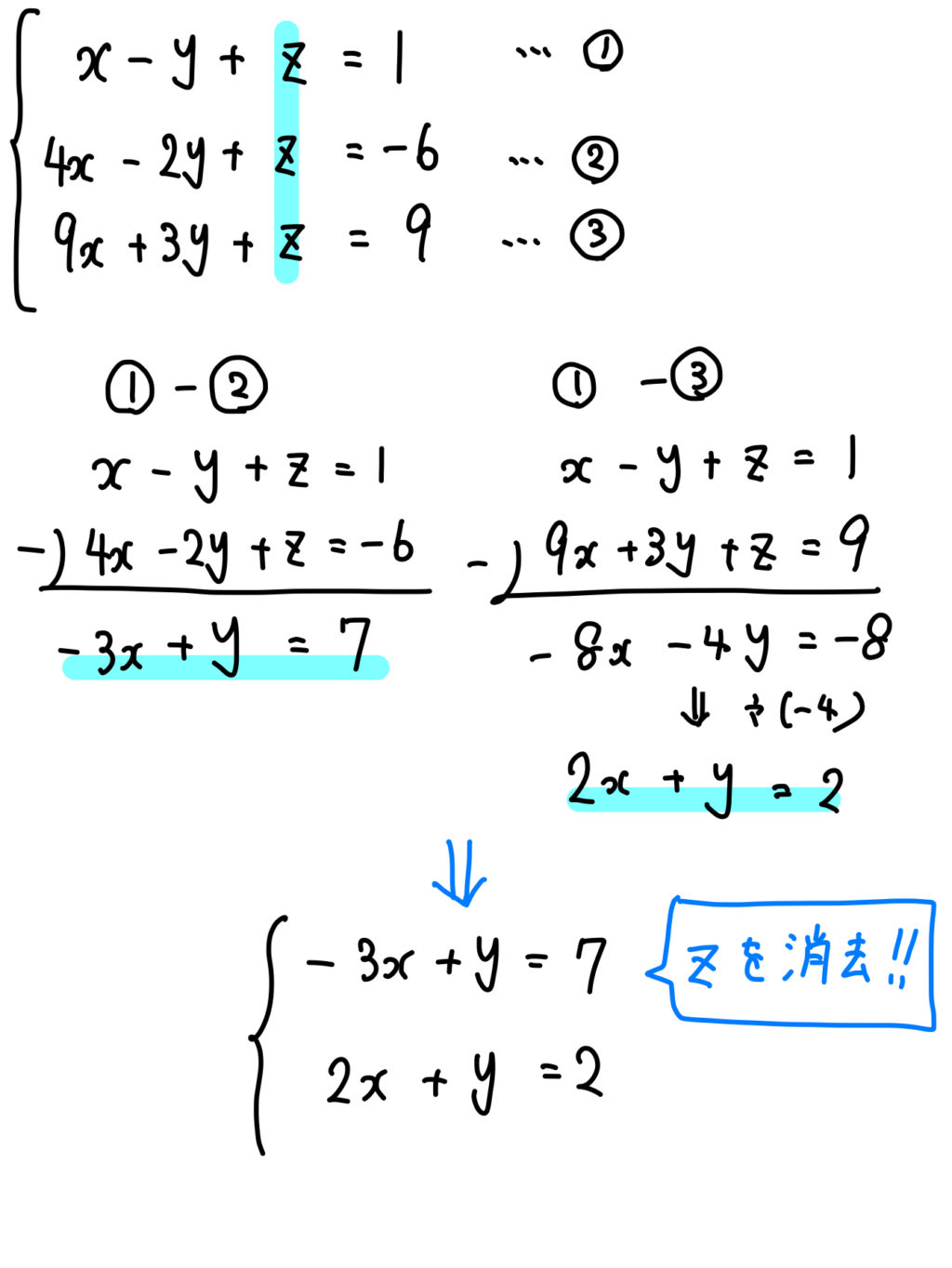
高校数学で学習する連立方程式の解き方まとめ 数スタ

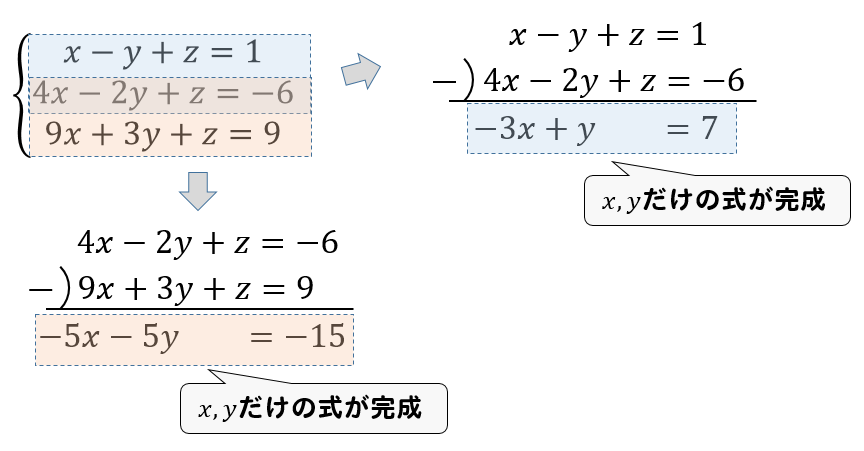
連立方程式３つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト

トップ100連立方程式公式 最高のカラーリングのアイデア

連立方程式の例題部分を教えてください 連立方程式の解き方を教 Yahoo 知恵袋

Math 超簡単 連立方程式の利用 働きアリ

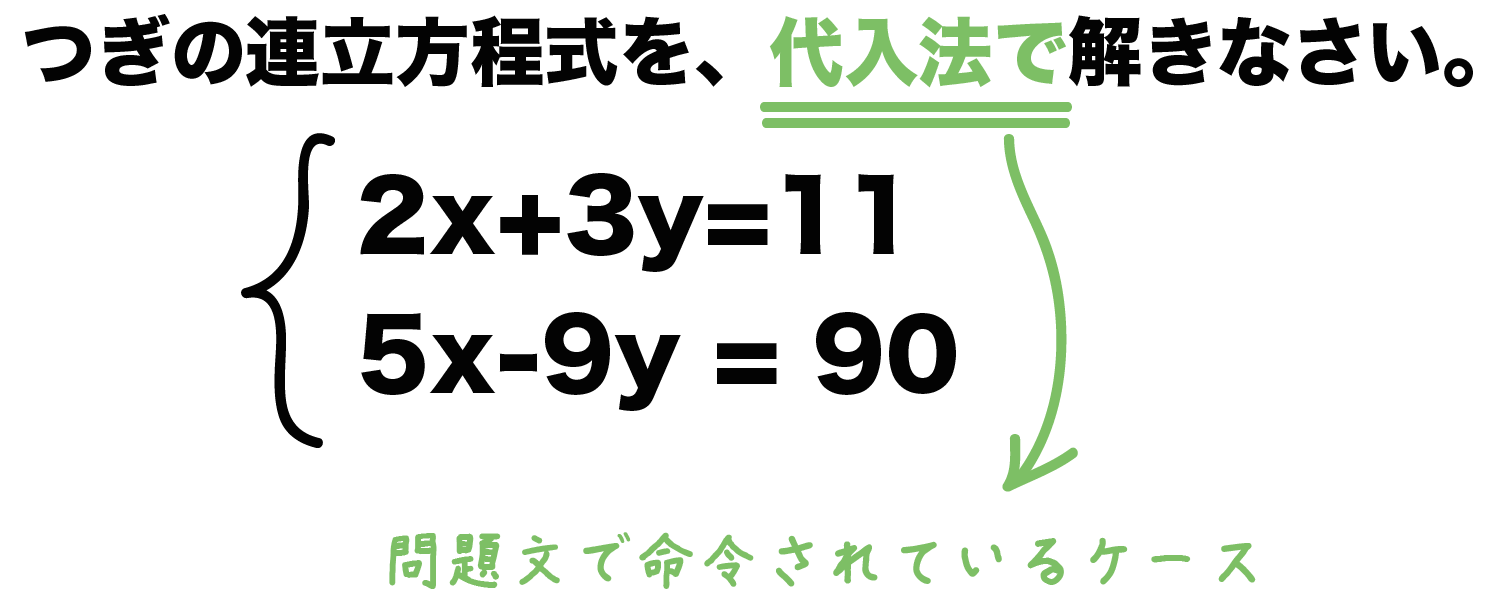
超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく

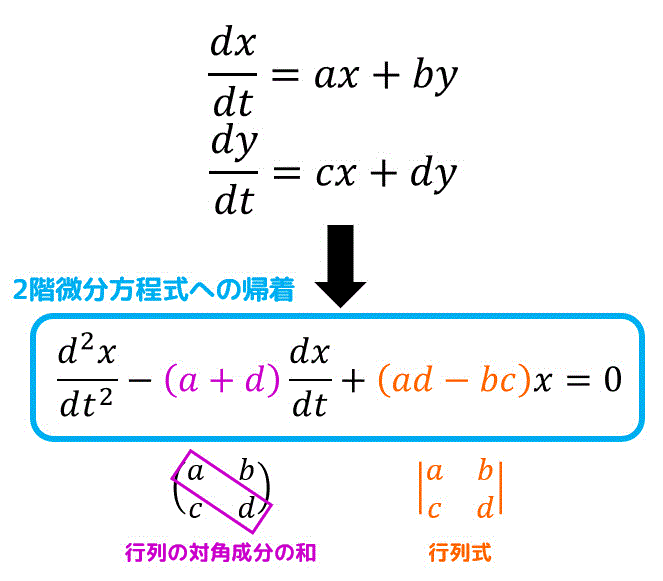
うさぎでもわかる微分方程式 Part10 連立微分方程式 2階微分方程式に帰着させて解くパターン 工業大学生ももやまのうさぎ塾

連立方程式 A B C の形をした方程式の解き方をイチから解説 Youtube

鉄則９ 方程式 連立方程式 １次 寺田の数学合格鉄則96に関するメモ

中２連立方程式の解き方と計算問題 代入法と加減法 Irohabook

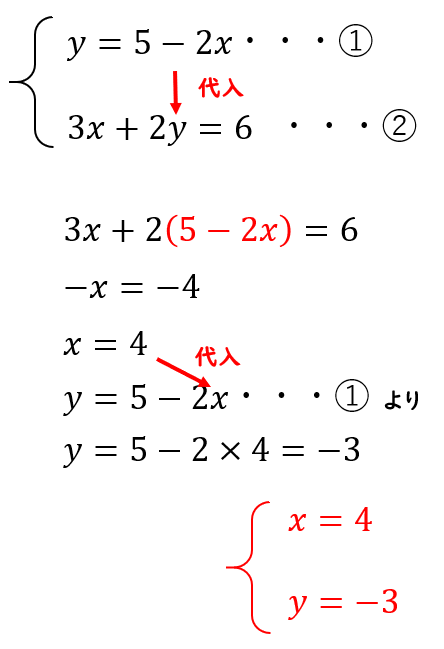
連立方程式の2つの解き方 代入法 加減法 数学fun

連立方程式 問題 Youtube

中２連立方程式の解き方と計算問題 代入法と加減法 Irohabook

連立方程式の2つの解き方 代入法 加減法 数学fun

例題 克拉瑪公式解二元一次方程組 Youtube

第1章 連立方程式

App Store 上的 中2連立方程式計算問題

連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料

1

中２連立方程式の解き方と計算問題 代入法と加減法 Irohabook

鉄則１０ 方程式 連立方程式 一般 寺田の数学合格鉄則96に関するメモ

均一影片 例題 解二元一次聯立方程式 綜合應用1 學習單 Shareclass

連立3元1次方程式 まなびの学園

二元一次方程式圖形

連立方程式で 例題のように より や X 2を に代 Yahoo 知恵袋

小数点の連立方程式 解き方をイチから解説してくぞ 中学数学 理科の学習まとめサイト

高校数学で学習する連立方程式の解き方まとめ 数スタ

連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学

中学２年生 数学 連立方程式 文章題 速さ On Vimeo

ちょっと複雑な連立方程式を練習しよう インターネット家庭教師のアスミラ

Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download

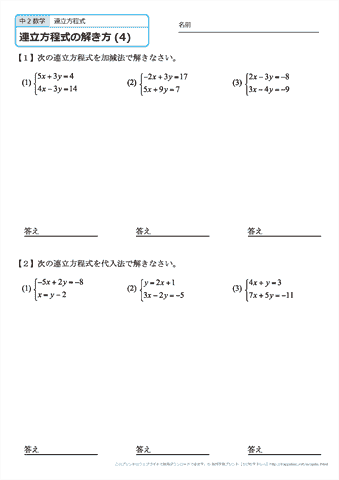
中学２年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

一元三次方程式試誤法例題 三角函數 利用三角函數求解一元三次方程式 Pripdw

E 微分例題微分方程 Rjhi

Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download

理工系の数理 線形代数 Toshitaka Nagai Atsushi Nagai Junkichi Satsuma Takeo Fujiwara Masayasu Mimura Amazon Com Books

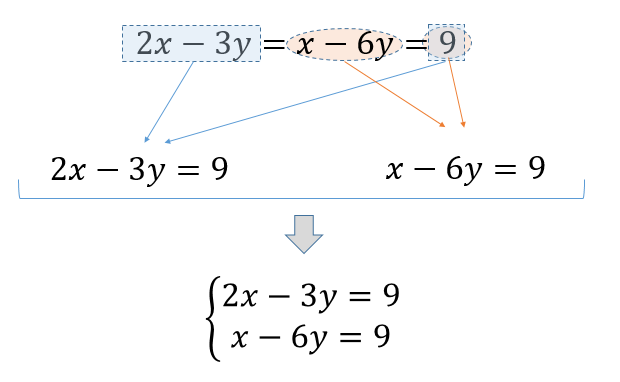
連立方程式３つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト

Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download

測評網 國一下 數學第一次段考 複習錦囊

C Pp 1617 Include Stdio H Include Math

無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア

みかん海老 ありがとうございます やはりその時次第で臨機応変にしろという事ですね センターでやった例題の連立方程式がマイナスばかりだったので困惑しておりました

加減加減 Vsqhy

中学数学 連立方程式 計算問題 For Android Apk Download

3种方法来解包含两个变量的代数方程组

中2 数学 連立方程式の解き方二通りを解説 授業動画あり アオイのホームルーム

3种方法来解包含两个变量的代数方程组

連立方程式の文章題 第２講 例題 清水塾

高校入試 解き方 が身につく問題集 数学 Amazon Com Books

第1章 連立方程式

例題付き 連立方程式の解き方と失敗しないコツ

100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア

トップ100連立方程式公式 最高のカラーリングのアイデア

中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット

最も共有された 三連立方程式 犬イラスト

数学知能 推荐一个解答方程式 2元一次 各种方程式 结果的网站wolfram Com Steemit

例題 解二元一次聯立方程式 綜合應用3 數學 均一教育平台

二元二次方程式定義連立方程式とは Gjlni

中2数学 連立方程式とは 例題編 映像授業のtry It トライイット

中2連立方程式 A Bを含む連立方程式の解が等しい場合 Youtube

トップ100連立方程式公式 最高のカラーリングのアイデア

うさぎでもわかる微分方程式 Part10 連立微分方程式 2階微分方程式に帰着させて解くパターン 工業大学生ももやまのうさぎ塾

2元一次方程式題目初中數學 二元一次方程式 例題2 Gquhm

例題 解二元一次聯立方程式 綜合應用1 數學 均一教育平台

3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく

コンピュータ機械工学

二階微分方程式一般解定數係數の二階線型同次微分方程式の解法 Qwvatk

連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典

二元一次聯立方程式

三元一次方程式例題 B Cvyup